DIGITAL CONTROLLER SYSTEM INTRODUCTION:
The development of process control has seen the blend of electronics technology into almost every aspect because of low cost, consistency, miniaturization and case of interface. It is natural that the further development of digital electronics and associated computer technology has brought about the rapid introduction of digital techniques in the field of process control. Some aspects of process control, such as the initial transduction of a controlled Variable into electrical information, will probably always be of analog nature. It is inevitable, however, with the continued development of computers, miniaturized digital electronics and associated technology that the evaluation and controller phase of process control may be digitally performed.
DIGITAL PROCESS CONTROLLERS:
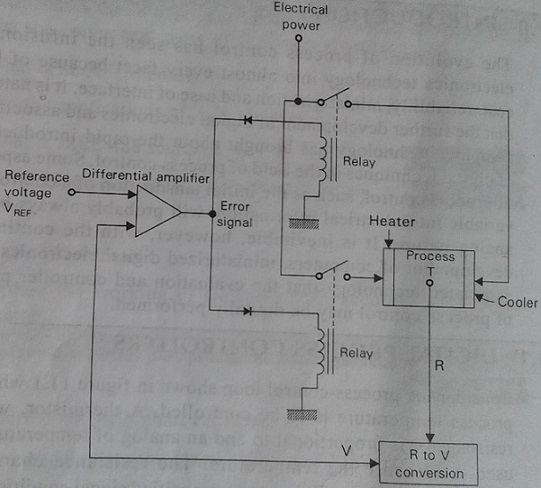
Consider the process-control loop shown in figure, where a process temperature is to be controlled. A thermistor, whose resistance R is proportional to and an analog of temperature, is used to measure the temperature. The resistance change is converted to a voltage V via some unspecified signal conditioning. This voltage is compared to some reference voltage (set point) by a differential amplifier (evaluation), the output of which activates either a heater or cooler. The range of allowed temperature is determined by the differential amplifier swing necessary to trip either relay. In this loop the temperature is represented by a proportional electrical signal. We then say that the electrical signal is an analog of the temperature. In the case of the thermistor, the resistance is an analog of the temperature.
In a similar fashion, in a pneumatic system, we may have a fluid pressure that is an analog of a variable. The analog relationship between processing signals and dynamic variables need not be linear and in many cases is not. The significant factor here is that the processing signal is a smooth and unique representation of the dynamic variable. In figure we see two examples of analog proportionalities between a variable c and an analog signal b. In case 1, we have a linear relationship and in case 2, a nonlinear relationship, but both are still analog representations of c.
 |
| The relationship between a Variable c and its measured equivalent b. |