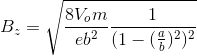Cylindrical Magnetron Derivation

Magnetron Oscillators:

A Magnetron Oscillator is used to generate high microwave power required in radar and communication systems. Magnetrons are cross field tubes in which the magnetic field and electric field are perpendicular to each other. All magnetrons consist of some form of anode and cathode operated in DC magnetic field which is perpendicular to DC electric field. Due to this cross field, electrons emitted from cathode moved in curved paths. If the magnetic field is strong enough the electrons will not arrive at the anode, but return to cathode itself. Thus the anode current is cut off. Magnetrons can be classified into three. They are

1. Split anode magnetron:

This type of magnetron uses negative resistance.

2. Cyclotron frequency magnetron:

This magnetron operates under the influence of synchronization between AC components of electric field and periodic oscillations of electrons in the direction parallel to the electric field.

3. Travelling wave magnetron:

This type of magnetron depends on the interactions of electrons with travelling electromagnetic field.

Cylindrical Magnetron Derivation:

Schematic Diagram of Cylindrical Magnetron

B_o - Flux Density
a - radius of cathode cylinder
b - radius of anode cylinder

Equation of Electron Motion or Hull cut off Voltage equation:

A charged particle in motion in a magnetic field of flux density B, experiences a force that is proportional to the charge, velocity, flux density and sine of angle between velocity and magnetic flux. The general equation for the motion of electron in terms of cylindrical co-ordinates is given as,

r²(dΦ/dt) = ½ω_cr² + constant ------------------ (1)

Where ω_c is the cyclotron angular frequency given by,

ω_c = eB_z/m

e – charge of electron

B_z – magnetic flux density

M – mass of electron

Let, r = a and dΦ/dt = 0

Therefore, Equation (1) becomes

½ω_ca² + Constant = 0

Constant = -½ω_ca² --------------------- (2)

Substitute equation (2) in (1)

r²(dΦ/dt) = ½ω_cr² - ½ω_ca² = ½ω_c(r² - a²)

dΦ/dt = ω_c(r² - a²)/2r² = ½ω_c (1- (a²/ r²)) ---------------- (3)

The KE of electrons is given by,

½mv² = eV

v² = 2eV/m

considering r and Φ components of electron velocity, the above equation can be represented as,

v_r² + v_Φ² = 2eV/m

(dr/dt)² + (r dΦ/dt)² = 2eV/m ---------------- (4)

Let r = b

V = V_o

dr/dt = 0

Therefore the above equation (4) becomes,

(b dΦ/dt)² = 2eV_o /m -------------------- (5)

Substituting dΦ/dt from eq (3)

b²(ω_c/2 (1- (a²/ r²)))² = 2eV_o /m

Substituting r = b

b²(ω_c (1- (a²/ b²)))² = 2eV_o /m

b²ω_c/4(1- (a²/ b²))²= 2eV_o /m

b²ω_c²(1- (a²/ b²))²= 8eV_o /m

Substituting ω_c = eB_z/m

b²(eB_z/m)²(1- (a²/ b²))²= 8eV_o /m

b²e²/m² (1- (a²/ b²))² B_z² = 8eV_o /m

This magnetic field intensity is known as cut off flux density, B_oc

V_oc = b²e B_z² (1 –(a/b)²)²/8m

This equation is known as ‘Hull cut-off voltage equation’

Cyclotron Angular Frequency:

The cyclotron angular frequency of cylindrical magnetron is given by,

ω_c = eB/m

The period of oscillation is given by,

T = 2 π/ ω_c

T = 2 πm/eB

The phase shift is given by,

Φ = 2 πm/N

Where, N is the number of cycles.

Output Power and Efficiency:

The efficiency and output power of the magnetron depend on the structure and power supply. The equivalent circuit of magnetron is,

Y_e – admittance

C – Capacitance

L – Inductance

G_r – Resonator Conductance

G_l – Load Conductance

The unloaded quality factor is given by,

Q_un = ω_oC/G_r

The loaded quality factor is given by,

Q_l = ω_oC/G_r+ G_l

The external quality factor,

Q_ext = ω_oC/G_l

The circuit efficiency, η_c = 1/(1 + (Q_ext/Q_un))

Electronic efficiency, η_e = (V_oI_o – P_lost) /V_oI_o

Where V_O – Anode Voltage

I_o – Anode Current or Beam Current

P_lost – Power lost in the anode.