Having seen the focusing system we now study the deflecting system used in cathode ray tube. There are two sets of deflecting plates. These plates will be supplied with the appropriate voltages that make out a pattern on the screen. The effect of applying a voltage to the deflecting plates is discussed below. We have to recollect the motion of a charged particle in an electric field to understand the phenomenon of deflection, called the electrostatic deflection in CRT.
The following figure shows the arrangement for the electrostatic deflection. There are two parallel plates with a potential in between them. A uniform electric field is produced by the plates, in the Y direction. Therefore any electron entering in this field will experience a force in the Y direction. Therefore it will be accelerated in that direction. There will be no force acting either in X direction or Z direction. As such there will be no acceleration of the electron in these directions.
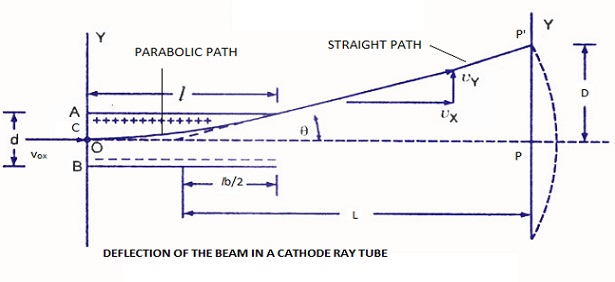 |
| Electrostatic Deflection in CRT |
Let Ea = voltage of pre-accelerating anode; V
e = charge of an electron; C
m = mass of the electron; kg
vox = initial velocity of the electron entering the deflecting plates; m/s
Ed = potential between deflecting plates; V
d = distance between deflecting plates; m
ld = length of the deflecting plates; m
L = distance between screen and the centre of the deflecting plates; m and
D = deflection of electron beam on the screen in the direction Y; m
The loss of potential energy when the electron moves from cathode to accelerating anode
PE = eEa
The gain in kinetic energy by the electron is
KE = ½ mvox2
Equating the two energies, we have
vox = (2eEa/m)½
This is the velocity of the electron in the X direction when it enters the deflecting plates. The velocity in the X direction remains the same throughout the passage of electrons through the deflecting plates as there is no force acting in this direction.
The electric field intensity in the Y direction is fy = Ed/d
The force acting on the electron in Y direction is
Fy = eƐy = e(Ed/d)
Suppose ay is the acceleration of the electron in Y direction
Fy = m ay
Therefore ay = e Ɛy /m
There is no initial velocity in the Y direction so the displacement at any instant 't' in the Y direction is
Y = ½ ayt2 = ½ (e Ɛy /m)t2
As the velocity in X direction is constant, the displacement in X direction is given by,
x = voxt
t = x/vox
Substituting the above value of t, we have
Y = ½(e Ɛy /mvox2) x2
The just above Equation is of a parabola.
The slope at any point (x, y) is
dy/dx = (e Ɛy/mvox2) x
Substituting the value ld in above given equation, the value of tan q is
tan θ = (e Ɛy /mvox2)ld = eEd ld / mdvox2
The electron after leaving the deflecting plates travels in a straight line path leaving the parabolic path. This is because of the fact that it crossed the electric field that influenced its motion. However the straight line path is tangential to the parabolic path at x =ld and the tangent intersects the line which is X axis at a point O'. The location of this point is given by.
x, O' = y / tan θ = (e Ɛy ld2 / 2mvox2) / e Ɛy ld / mvox2 = ld / 2 (m)
The apparent origin O' is at the centre of the deflection plates from the equation. The deflection D on the screen is given by
D = L tan θ = L eEd ld / mdvox2 (m)
Substituting the value vox2= 2eEa/ m in equation
we have
D = (Le EdLd / md) (m / 2eEa) = (LldEd / 2dEa) (m)
From the above equation the following conclusions can be made :
1. For a given accelerating voltage Ea, and for given dimensions of the CR Tube, the deflection of the electron beam is directly proportional to the deflecting voltage. This means that the CRT may be used as a linear indicating device.
2. The deflecting voltage is assumed as a fixed voltage in the explanation above. Practically the deflecting voltage is a time varying quantity and the image on the screen thus follows the variations of the deflection voltage in a linear manner.
3. The deflection is independent of the e/m ratio. In CR Tube negative ions such as oxygen, carbon, chlorine etc. are also present. As deflection is independent of e/m in an electrostatic deflecting system the ions travel with the electrons and are not concentrated at one point. Therefore there is no possibility of the ion burn in a CR Tube employing electrostatic deflection.
Deflection sensitivity: It is defined as the deflection of the beam on the screen per unit deflection voltage.
Deflection sensitivity is abbreviated as `S'
Therefore S = D / Ed = Lld / 2dEa meter / volt
Deflection factor of a CR Tube: It is defined as the reciprocal of the deflection sensitivity. It is abbreviated by letter 'G'.
Therefore deflection factor G = I / S = 2dEa/ Lla V/m
The deflection sensitivity can be increased by decreasing the accelerating voltage Ea as is seen from the definition of deflection sensitivity. This results in reduced luminosity of the spot. In converse a high value of Ea produces more acceleration of the beam and gives a bright spot. Increasing the accelerating voltage necessitates large deflection potential on the deflecting plate, to produce a given displacement. Highly accelerated beam is difficult to deflect and is termed hard beam. Typical deflection sensitivity of CR Tube ranges from 0.1 mm/V to 1 mm/V. This corresponds to the deflection factor values in the range 10 V/m and 1V/m.
Tags:
Cathode Ray Oscilloscope
