Implicants
Let an SOP function be expressed in the form
In Eq. (2.28), we have four product terms on the RHS. Let any one or more of the above four terms give an output of 1. Then, this implies that f = 1. For example, if x1x2x4 = 1, then f = 1. Similarly, when x1′x2x3x4 = 1 or x1x2x3x4 = 1, then also f = 1, and so on. Thus each one of the above terms is an implicant. Notice also that a minterm will be an implicant, but an implicant need not be a minterm. For example, the terms x1x2x3x4 and x1′x2x3x4 are implicants as well as minterms. But, the implicants x1x3x4 and x1x2x4 are not minterms.
Prime Implicants
Figure 2.26 highlights the implicants as A, B, C, D, and E, respectively. The corresponding minterms are a'cd, abd, ab’c, bc'd, and acd, respectively. Of the five implicants, all are prime implicants. However, implicants D, and E are not essential, as the minterms in them are already covered by A, B, and C. These prime implicants are called redundant terms.
Let an SOP function be expressed in the form
f(x1, x2,…, xm) = x1x2….xn + x1x2….xm (2.27)
Let, at least, any one of the product terms, say, x1, x2, x3, …, xm = 1. Then, we observe that the given function f(x1, x2, x3, …, xm) = 1. In such a case, we call the product term x1, x2, x3, …, xm as an implicant of the given logic function f(x1, x2, x3, …, xm).
We now define the term implicant. Let f(x1, x2, x3, …, xm) be an m-variable SOP function and S be the product term x1x2….xn in that function. We now state that S is an implicant of the function f if and only if the value S is equal to 1 so that the value of the function f is also equal to 1. It can be seen that this definition is quite lengthy. To explain this, consider the following example. Let
f(x1, x2, x3, x4) = x1′x2x3x4 + x1x2x3x4 + x1x2x4 + x1x3x4 (2.28)
In Eq. (2.28), we have four product terms on the RHS. Let any one or more of the above four terms give an output of 1. Then, this implies that f = 1. For example, if x1x2x4 = 1, then f = 1. Similarly, when x1′x2x3x4 = 1 or x1x2x3x4 = 1, then also f = 1, and so on. Thus each one of the above terms is an implicant. Notice also that a minterm will be an implicant, but an implicant need not be a minterm. For example, the terms x1x2x3x4 and x1′x2x3x4 are implicants as well as minterms. But, the implicants x1x3x4 and x1x2x4 are not minterms.
If an implicant must make a function equal to 1, then a term that makes a function equal to 0 is not an implicant of that function. Consider the function
f (a, b, c, d)= abd + abc + acd (2.29)
In this function, whenever b = d = 0, f = 0. This means that the term b'd' is not an implicant of f.
Prime Implicants
A prime implicant is an implicant from which if we delete any variable (or literal), then it can no longer be considered as an implicant. For example, consider the term abd in Eq. (2.28). From this equation, if we remove any one of the terms (i.e., a, b, or d), then the resulting product term will no longer imply f. That is, if a is removed, then the resulting term bd is no longer an implicant of the function f. Then, we say that the term abd is a prime implicant of f. Similarly, the other terms (i.e., abc and acd) are also prime implicants of f.
Essential Prime Implicant
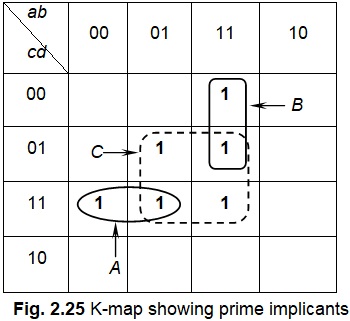
A prime implicant is said to be essential, if a minterm in an SOP expression is covered by only one prime implicant. For example, let us consider the K-map shown in Fig. 2.25. We find that minterm m2 is covered by prime implicant A only. So, we call A as an essential prime implicant. Similarly, minterm m12 is covered only by prime implicant B, and hence B is an essential prime implicant. We also find that minterms m5 and m15 are not covered by any other prime implicants; hence C is also an essential prime implicant. Summarizing the discussions, we may now state that:
- Any minterm or combinations of minterms, which make an SOP function equal to 1 is an implicant.
- If, from an implicant, a literal removed makes it not to be a member of the function, it becomes a prime implicant.
- In a reduced function, if the removal of a prime implicant changes the structure of the function, then that prime implicant is essential in forming the function.
Figure 2.26 highlights the implicants as A, B, C, D, and E, respectively. The corresponding minterms are a'cd, abd, ab’c, bc'd, and acd, respectively. Of the five implicants, all are prime implicants. However, implicants D, and E are not essential, as the minterms in them are already covered by A, B, and C. These prime implicants are called redundant terms.



Really really helpful couldn't find such consize explanation.
ReplyDelete