Binary Subtraction with Examples:
Binary subtraction is performed in the same way we perform decimal subtraction. There are two methods for decimal and binary subtraction. In the first method, we use direct subtraction. In the second method, we use an indirect subtraction method called complement’s method. We first discuss the direct subtraction.
Direct Subtraction
In this scheme, we subtract a smaller number from a larger number. This is illustrated using an example of decimal subtraction.
Example 28: Subtract decimal number 657 from decimal number 725.
Solution: To subtract, we write the numbers one below the other as shown in Table 1.33. Then we first subtract the least-significant digit (LSD) 7 from LSD 5. This subtraction is not possible. Therefore, we borrow a 1 from digit 3 in the second bit position and transfer it to LSD position. When this reaches LSD, it gains a weight of 10 and we add this to LSD 5 to make it 10+5 = 15. We can now subtract 7 from 15 to yield the difference 8 in the LSD position.
We then move to the second digit position of 3. Since a 1 was borrowed from this place to LSD, we have only a 2 remaining in this position. We now try to subtract 5 from 2 and this is not possible. Therefore, as in the previous case, we borrow a 1 from the most significant digit (MSD) position and add the new weight of 10 to 2 to make it 12. We can subtract 5 from 12 to yield the difference of 7 in the second digit position, as shown in Table 1.34.
Finally, we notice that when a 1 is borrowed from the MSD, the digit remaining there would be 6 and 6 ‒ 6 = 0 as the difference in MSD.
Binary subtraction is performed in the same way we perform decimal subtraction. There are two methods for decimal and binary subtraction. In the first method, we use direct subtraction. In the second method, we use an indirect subtraction method called complement’s method. We first discuss the direct subtraction.
Direct Subtraction
In this scheme, we subtract a smaller number from a larger number. This is illustrated using an example of decimal subtraction.
Example 28: Subtract decimal number 657 from decimal number 725.
Solution: To subtract, we write the numbers one below the other as shown in Table 1.33. Then we first subtract the least-significant digit (LSD) 7 from LSD 5. This subtraction is not possible. Therefore, we borrow a 1 from digit 3 in the second bit position and transfer it to LSD position. When this reaches LSD, it gains a weight of 10 and we add this to LSD 5 to make it 10+5 = 15. We can now subtract 7 from 15 to yield the difference 8 in the LSD position.
We then move to the second digit position of 3. Since a 1 was borrowed from this place to LSD, we have only a 2 remaining in this position. We now try to subtract 5 from 2 and this is not possible. Therefore, as in the previous case, we borrow a 1 from the most significant digit (MSD) position and add the new weight of 10 to 2 to make it 12. We can subtract 5 from 12 to yield the difference of 7 in the second digit position, as shown in Table 1.34.
Finally, we notice that when a 1 is borrowed from the MSD, the digit remaining there would be 6 and 6 ‒ 6 = 0 as the difference in MSD.
The steps described above can be used for direct subtraction of smaller numbers from larger numbers. Hence, we will adopt the same procedure to perform binary subtraction. As in the case of binary addition, for subtraction also we prepare subtraction tables. Table 1.35 shows the 2-bit subtraction, and Table 1.36 shows the 3-bit subtraction.
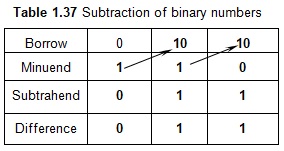
Example 29: Subtract binary number 110 from binary number 1110.
Solution: To subtract, we write the numbers one below the other as shown in Table 1.37.