Two methods are used for converting decimal numbers to their equivalent binary numbers.
Conversion Using Division
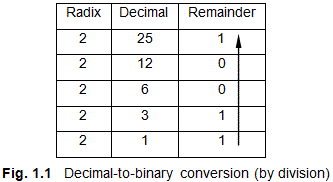
Example 1: Convert (25)10 into equivalent binary number.
Solution: The procedure using division is illustrated in Fig.1.1. In this, we divide the given number repeatedly by 2. In each division, if the number is exactly divisible by 2, we put a 0 as remainder against the number on its right-hand side. If the number is not exactly divisible by 2, we put a 1 as the remainder. We proceed like this up to the last digit, as shown in Fig. 1.1. We then read upwards, in the direction of the arrow shown to get the required binary number.
From the Fig. 1.1, we find the binary equivalent of decimal number as
(25)10 = (10011)2
Check: (11001)2 = 1 ´ 24 + 1 ´ 23 + 0 ´ 22 + 0´21+ 1 = 16 + 8 + 1 = (25)10
Example 2: Convert decimal numbers (a) 221 and (b) 10120 into equivalent binary numbers.
Solution: Instead of going into long division process, a very easy and simple method of decimal-to- binary conversion is given below.
(a) In this method, we first find the powers of 2 which add up to yield the given number. We know that 27 = 128 and 28 = 256. Since 221 is less than 256, we conclude that 221 = 128 + some numbers which are lower powers of 2. To find these, we subtract 128 from 221, which yields
221 ‒ 128 = 93
The nearest power of 2 is 64. Subtracting this from 93, we get
93 ‒ 64 = 29
Proceeding in this way, successive subtraction shows that
29 = 16+8+4+1
Thus the given number is decimated as:
221 =128+64+0×32+16+8+4+0×2+1 = 11011101
where we have substituted 0s in the places of 32 and 2, respectively, as these two numbers are absent in the summation.
(b) Decimating 10120, we find that”
10120 = 8192+1024+512+256+128+8
= 10001110001000
Conversion by Tabulation
This is an extension of the fist method explained illustrated in Example 1.
Example 3: Convert decimal number (83)10 into its binary equivalent by the tabulation method.
Solution: In this method, we first prepare Table 1.1, which is the decimal-to-binary conversion table. Table 1.1 has 7 columns (this number depends on the number of divisions we have to perform and 4 rows (fixed).
In Table 1.1, the first step is to enter the decimal number to be converted into binary (in this case 83) into Column 1 of Row 1 as shown. The second step is to enter the radix of the number system to which conversion is required into all the columns of Row 2. Here, conversion is required into the binary system and hence its radix 2 is entered into all the columns of Row 2, as stated.
The third step is to divide 83 by radix number 2. We notice that 83 is not fully divisible by 2. 83 divided by 2 yields 42 as quotient and 1 as remainder. These are the respective entries in column 1 of Rows 3 and 4. Summarizing the operations described above, we find that the entry under Column 1, Row 1 is 83, Row 2 is 2, Row 3 is 42, and Row 4 is 1.
The next step is to enter number 42, the quotient of the first division, into Column 2, Row 1 as shown in Table 1.1. Proceeding as above, 42 is divided by radix 2. This operation yields a quotient of 21, and a remainder of 0; we enter 21 in Row 3 and 0 in Row 4 under Column 2 of table 1.1, as shown. In the table, we have used slashed arrows to indicate the transfer of quotient numbers and vertical arrows to denote the direction of division operation. For example, the first and rightmost slashed arrow indicates the transfer of the first quotient number 42 to Column-2, Row-1 cell, as shown in Table 1.1. The first vertical arrow 1 indicates that division of 83 by 2 gives 42 as the quotient and 1 as the remainder. These vertical transfers are also shown in Table 1.1.
We find that 42 becomes the next (second) entry to be divided by radix 2. The division yields the quotient as 21 and remainder as 0, since 42 is fully divisible by 2. As the next step, we divide 21 by 2 in Column 3. The results of this and subsequent operations described above are indicated in Table 1.1. We stop the division and associated operations in Column 7 (for this problem) when the remainder becomes 1 and no further division is possible.
Reading the entries in Row 4 (remainder row), rightwards, we find
(83)10 = (1100101)2